F. Wagner March 2006
StateWORKS: What's All This State Machine Stuff?
Definitions
The finite state machine, also called finite automaton or just state machine is often misused and misunderstood. We have already written a paper about it [1] but it seems that the topic requires still further discussion. This technical note handles state machine models only and is taken from the book [2].
If we take two books which have in their title "Automata Theory" but one book is written for hardware designers and the other one for software people we get the impression that there are two different Automata Theories. The hardware book is about digital system design. The software book is about the mathematical description of computation, especially programming languages. Both use the concept of state machine as the basis of their methods and theorems but the terminology and the emphasis are completely different:
- in hardware design a state machine is a vehicle for a design method,
- in software a finite automaton is a means to prove theorems.
Unfortunately, software is not only theory of computation. When developing software applications, programmers also use the state machine concept to control or model behaviour.
The finite state machine introduces the concept of a state as information about its past history. All states represent all possible situations in which the state machine may ever be. Hence, it contains a kind of memory, about how the state machine can have reached the present situation. As the application runs the state changes from time to time, and outputs may depend on the current state as well as on the inputs. Let us now make a review how that concept is understood in different technical and scientific environments.
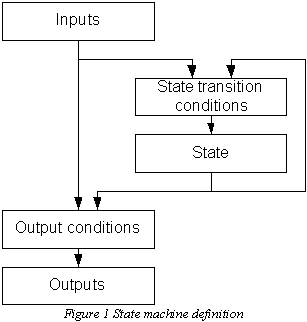
A control system determines its outputs depending on its inputs. If the present input values are sufficient to determine the outputs the system is a combinational system, and does not need the concept of state. If the control system needs some additional information about the sequence of input changes to determine the outputs the system is a sequential system. The logical part of the system responsible for the system behaviour is called a state machine. Sometimes, combinational systems are treated separately and sometimes they are considered as a kind of degenerate state machine. To keep things simple, we shall call any logic that determines a system behaviour a state machine. According to this definition, a state machine can be represented by the diagram in Figure 1. The history of input changes required for clear determination of the state machine behaviour is stored in an internal variable State. Both, the State transition conditions and the Output conditions are functions of Inputs and a State.
Presentations - Transition matrix
A state machine changes states. Therefore we need a presentation to show the state changes. There are two basic presentations: transition matrix and state transition diagram, which are used for that purpose.
The transition matrix may have two forms shown as in Table 1 and Table 2 which is a specification of the behaviour of a counter (or timer). You should note a very important point: this counter will, of course, be counting something, and the following tables do not bother to show it! In fact, we are not really concerned about the actual counting process, which we take for granted, but are very interested to see such things as when the counter reaches a certain limit, or whether it is disabled or enabled. So what we are discussing is not the actual counter, which is of course a form of state machine, but rather the control features of the counter. The transition matrix in Table 1 defines inputs which cause transitions. Normally, inputs are considered a single condition (event). If there are multiple inputs which cause the same transition the table has several "From" lines for the same state. Alternatively, a boolean condition could be written into the table. A more complex transition condition may require an additional verbal explanation (see the "expiration" signal).
Table 1 Transition matrix: variant 1
| To From |
RESET | STOP | RUN | OVER | OVERSTOP |
| RESET | Start | ||||
| RESET | ResetStart | ||||
| STOP | Start | ||||
| STOP | ResetStart | ||||
| RUN | Reset | Stop | "expired" | ||
| OVER | Reset | ResetStart | Stop | ||
| OVERSTOP | Reset | ResetStart | Start |
Note:"expired" happens when the Counter Value becomes equal to the Counter Constant.
The second variant of the transition matrix shown in Table 2 defines the "next states" as a function of the present state and inputs.
Table 2 Transition matrix: variant 2
| Input State |
Reset | ResetStart | Start | Stop | "expired" |
| RESET | RUN | RUN | |||
| STOP | RUN | RUN | |||
| RUN | RESET | STOP | OVER | ||
| OVER | RESET | RUN | OVERSTOP | ||
| OVERSTOP | RESET | RUN | OVER |
Outputs (Actions)
Most applications require some actions to be performed (outputs); actions required by the controlled system. Note that in hardware design the term "output" is used, while for software design the term "action" is more popular. Several types of actions can be defined depending on the conditions and moment they are performed:
- Entry Action
- Exit Action
- Input Action
The Entry Action is an action done when the state machine enters a state.
The Exit Action is an action done when the state machine leaves the state.
The Input Action is an action done when an input (condition) is true. Each state has its own set of Input Actions. Input Actions that are done in any state (effectively state independent) are also used.
Theoretically, we could use also a Transition Action performed during the state change. Note that though similar to them it is neither an Entry Action nor an Exit Action which are both state dependent; the Transition Action is transition dependent. The Transition Action does not play any role in state machines: in many cases an Input Action with the condition equal to a transition condition could be treated as a Transition Action. A more detailed discussion would show that this arrangement does not correspond fully to a Transition Action definition. Anyway, it seems that that the Entry, Exit and Input Actions are sufficient for a state machine specification.
We use various Actions to make a state machine design understandable, and we apply certain rules. If a state machine changes state, all actions: Input, Exit and Entry Actions are carried out in this sequence but practically in the same moment. Without a state change only an Input Action may be performed.
A transition matrix may contain a definition of Input Actions in the form shown in Table 3. For instance, if in the state State_i the Input_condition_in is due the Input_Action_in will be carried out and the state machine goes to the state State_n. Also in that case the conditions specified in the table are often complemented by comments which specify the details of the conditions (see the comments for Input Action_kn).
In principle, the transition matrix is not used to define other actions though theoretically it would be feasible. For instance, we could add the Entry Action to the column captions specifying states.
Table 3 Transition matrix with Input Actions
| To From |
… | State_n | … |
| … | … | … | … |
| State_i | … | Input condition_in / Input Action_in | … |
| State_k | … | Input condition_kn / Input Action_kn1) | … |
| … | … | … | … |
1) If something is enabled
A transition matrix is considered as an informal method and as such is not treated very seriously. It is mainly used in situations where somebody wants to expose events which cause transitions. For instance, it is a sufficient means for defining the behaviour of a timer as shown in Table 1. It is difficult to make a complete specification of an application's behaviour using a transition matrix. Conditions which need to be explained in comments are by definition error prone and require interpretations.
The definition of a transition matrix is not quite precise and interpreted according to the situation: this is a typical characteristic of verbal specifications.
Presentation - State transition diagram
A state transition diagram is a graphical representation equivalent to the transition matrix. The state transition graph uses two elements: a circle to denote the state and an arc for the transition. (Technically, for mathematicians, the circles represent vertices and the lines represent edges of a directed graph.) In a simple diagram the arcs might be straight lines. The transition condition is written over the arc. The state transition diagram for the counter is shown in Figure 2.

A transition matrix is a table and therefore in some situations it is easier to draw than a graph. On the other hand, a state transition diagram is more readily comprehensible than a transition matrix. In the case of the counter example both presentations show the same information and are 100% equivalent.
The main task of a state machine is to generate actions. Unfortunately, neither a transition matrix nor a state transition diagram can show all design details of a state machine with actions. In such a case we need another presentation means.
Presentation - State transition table
Existence of actions complicates the presentation problem. Using a transition matrix or state transition diagram it is difficult to express the functionality of a state machine with several actions. Therefore, we use a state transition table as the most versatile tool for expressing the complete specification of a state machine.
We use a state transition table shown in Figure 3. The table contains fields to specify Entry, Exit and Input Actions.
Each State has its state transition table. The table consists of several fields used to specify actions and transitions. Each Action field may contain several Actions. A table may contain several Input Action expressions consisting of related Input_Action_Condition and Input_Action fields. Similarly, a table may contain several Transition expressions consisting of several Next State and Transition_Condition fields. In the condition fields we will use two boolean operators: AND (represented by &) and OR (represented by |) to define more complex logical expressions. The usage is as intuitively understood:
this_control_value & that_control_value or
this_control_value | that_control_value.
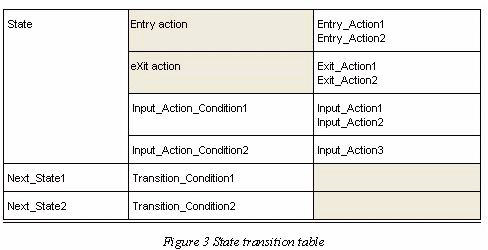
If the state transition table is to express completely the behaviour it should also have well defined priority rules for Transitions and Input Actions. The rule for transitions is obvious: as it is impossible to make more than one transition at the same time we agree that the sequence in the table determines the priority. For instance, if both: Transition_Conditions1 and Transition_Conditions2 are true the transition to Next_State1 will be performed.
The priority rule for the Input Actions is not so obvious and depends on the execution environment. If we assume that all Input actions that are due will be performed then their sequence in the table must not play any role. Otherwise we would try to realise a control sequence by prioritising Input Actions which is reserved for state machine only. The priority would be important if the execution environment performs only one Input Action at any one time.
Mathematical presentations
A finite state machine is also a standard model used in the mathematical foundation of computer science, like for instance in the formal specification of programming languages. Those concepts are event driven "Parser" problems. That fact explains at least partly the popular understanding of a state machine in software.
From that perspective a finite state machine (see for instance [3]) a finite state machine is a quintuple <Σ, S, s0, δ, F>, where:
- Σ is the input alphabet (a finite non empty set of symbols),
- S is a finite non empty set of states,
- s0 is an initial state, an element of S,
- δ is the state transition function: δ: S x Σ → S,
- F is the set of final states, a (possibly empty) subset of S.
A parser state machine is called also a recognizer or acceptor. Such a state machine has an initial and a final state and its path from the start to the final state is deterministic, i.e. there is only one transition from each state. We would rather say that all other inputs are ignored or by definition they cannot occur. If the state machine accepts several transitions from at least one state it is called nondeterministic.
Those kind of considerations are adequate for parsing of words but does not make sense for a control application outside that environment. We note also that that definition misses completely output (actions). That is understandable as the task of that state machine is to reach a final state which means that parsing has been successful; there is nothing to do on the way to that state. Theoretically, we could adapt that concept for our purpose - modelling applications implemented by software. It would require to us treat a state machine as an automaton that changes its state and than by decoding states we decide which actions are to be performed. That solution would be much more complicated as it is difficult to think separately about state changes and actions: state changes are in most cases the results of some feedback from the controlled application. It is a much simpler and more natural way to construct a state machine if we think at the same time about state changes and about actions to be done.
Staying in the world of symbols we can define a transducer finite state machine as a sextuple <Σ, Γ, S, s0, δ, ω>, where:
- Σ is the input alphabet (a finite non empty set of symbols),
- Γ is the output alphabet (a finite non empty set of symbols),
- S is a finite non empty set of states,
- s0 is an initial state, an element of S,
- δ is the state transition function: δ: S x Σ → S,
- ω is the output function.
If the output function is a function of a state and input alphabet (ω: S x Σ → Γ) that definition corresponds to the Mealy model. If the output function depends only on a state (ω: S → Γ) that definition corresponds to the Moore model.
The parser state machine model is useful for compilers. In a design of hardware digital circuits the transducer state machine, especially in the form of a Moore model is applicable.
Event driven model
Several software implementations based on the state machine concept assume that events are the only signals which can be used to control state machines, and implicitly that events which are not consumed (i.e. do not immediately provoke an action or transition) are discarded. That assumption means that states of a state machine must "store" not only the history of input changes (in a very compressed form) but the present value of inputs as well. In other words, the state transition diagram must contain explicitly all possible control paths. We discuss the problem in [1]. We mention here only that that kind of state machine interpretation is a nonsense, resulting for instance in a "state explosion" phenomenon.
Behaviour model and execution model
It is obvious that when specifying a state machine we should fully understand the required application behaviour. But there are two different goals of a behaviour specification.
The first goal is to make a specification which will serve as a base for developing software. Such state machine specifications are always informal, i.e. we describe approximately the behaviour: without a test there is no chance to find out errors in the specification. In addition, knowing that the specification will be coded, we are automatically not motivated to make the specification perfect. The coded implementation is then not a pure translation of the state machine specification into a code: it requires interpretation of the requirements, whereby the state machine specification is a kind of suggestion of how to make the skeleton of the behaviour but the true behaviour details are well hidden in the code.
A completely different situation arises if we specify a state machine which is intended to be executed directly, i.e. if we make an executable specification. By executable specification we mean a true executable specification, for instance using StateWORKS, where the specification result is carried out as is and it will never be coded. Such a specification is essentially different from the informal specification. Firstly, it must be perfect, i.e. it must fulfil all requirements. Secondly, it must take into consideration the features of the run-time systems that will carry out the specification. In other words, while specifying we have to think about the execution model which defines such things like: transition priorities, performing Input Actions, which actions are allowed, are multiple state transitions allowed, which actions are performed when entering the state, etc.
Why a state machine model is good?
There are a few ways to describe a behaviour of an application. The state machine concept is one of them. The beautiful thing about this concept is its power and simplicity. The power is the idea of a state as complete information about its past history. The simplicity is the presentation means: we need only a few notions to draw a state transition diagrams supported by state transition tables: a circle (state), an arc (transition) and actions (Entry, Exit, Input).
It does not mean that a specification of a state machine is just a simple thing. No, it can be quite difficult because making a behaviour specification is in general a difficult task. But by using a state machine concept, we have a chance to do it well.
Conclusions
We have discussed a definition and presentations of a state machine. We have shown that there are not several different concepts of state machines. There is only one concept which originally has come from Automata Theory. The specifics of jargon used in certain scientific or technical fields may engender the impression that a state machine concept for instance in hardware is different than in software. No, in all fields the definition of a state machine is exactly the same: a powerful and effective concept for behavior specification.
References
[1] Wagner, F., Wolstenholme, P., "Misunderstandings about state machines", IEE Computing & Control Engineering, August-September 2004.
[2] Wagner, F. et al., Modeling Software with Finite State Machines - A Practical Approach, Auerbach Publications, to be published in May, 2006.
[3] Caroll J., Long D., Theory of Finite Automata, Prentice Hall, New Jersey, 1989.

 download PDF version
download PDF version